
The Shape of a Raindrop
High in the atmosphere, water collects on dust and smoke particles in clouds. Raindrops start to form in a roughly spherical structure due to the surface tension of water. This surface tension is the "skin" of a body of water that makes the molecules stick together. The cause is the weak hydrogen bonds that occur between water molecules. On smaller raindrops, the surface tension is stronger than in larger drops. The reason is the flow of air around the drop.
As the raindrop falls, it lose that rounded shape. The raindrop becomes more like the top half of a hamburger bun. Flattened on the bottom and with a curved dome top, raindrops are anything but the classic tear shape. The reason is due to their speed falling through the atmosphere.
Air flow on the bottom of the water drop is greater than the airflow at the top. At the top, small air circulation disturbances create less air pressure. The surface tension at the top allows the raindrop to remain more spherical while the bottom gets more flattened out.
Even as a raindrop is falling, it will often collide with other raindrops and increase in size. Once the size of a raindrop gets too large, it will eventually break apart in the atmosphere back into smaller drops. This time, the surface tension loses and the large raindrop ceases to exist. Instead it pulls apart when it grows to around 4 millimeters or more.
The Scientific Formula
The slope of βe f f such that the same relation between Kdp /Nw and Do is preserved on average. Gorgucci et al. (2001a,b) developed algorithms for retrieving rain rate (R) as well as Do, Nw and m using βe f f in combination with the measurement pair (Zh, Zdr).
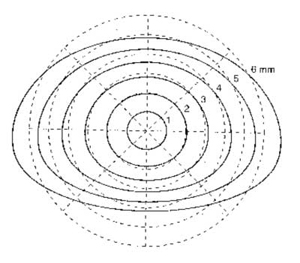
Equilibrium drop shapes for drop diameters of 1-6mm.
Thus Zdr is a direct measure of mass weighted median diameter. The functional relationship between Zdr and Do is developed from the underlying microphysical relation between the mean axis ratio of raindrops and their size. This shape size relation can potentially be perturbed in the presence of raindrop oscillations. Grogucci et al. (2002) developed a technique that watches the self-consistency between Zh, Zdr and specific differential phase Kdp, to account for the perturbation in oscillation, in retrieving Do from dual-polarization radar measurements.
Once Do is retrieved, then the other parameters of the DSD can be retrieved such as No of the normalized form of a Gamma distribution (Gorgucci et al., 2002). The statistics of the parameter Do, Nw are important in the development of algorithms.

